HP48/49 are able to find a solution y(T),
to a differential equation expressed as y'( T ) = f (T,y),
where the initial value of the function is given as y(to)=yo.
HP48/49 are able to solve differential equations in the numeric mode only.
|
Example:
Solve the Differential Equation
y' ( T ) = y + COS( T )
for y( 0 ) = 0 given that y( 0 ) = 0
1 - write the Differential Equation in the field f |
| |
2-Access Solve Application:
Press:
 [NUM SLV] if you are using HP49.
 [SOLVER] if you are using HP48.
and choose 2-Solve dif eq.. |
 |
| |
3 - write the Differential Equation
in the field f |
 |
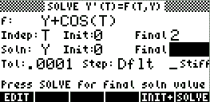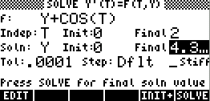
4 - enter independent
and dependent variables,
the limits and press [SOLVE]
|
 |
Press [ENTER]
to see the result in the stack
|
|
| |
|
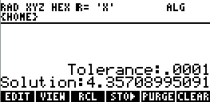
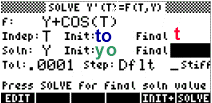
What are the variables enclosed?
|
Variables enclosed are to, t and yo
Given a differential equation y'( T ) = y + COS( T )
to solve it
for y( T ) given that y ( to ) = yo
the variables can be written
as in the picture beside.
|
|
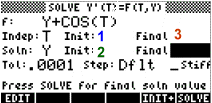
Example
Solve the Differential Equation
y'( T ) = y + COS( T )
for y( 3 ) given that y ( 1 ) = 2
Result:14.2307048559
|
 |